ABCDARIO DE LAS MATEMÁTICAS
Divulgación de las matemáticas: Ellas fueron las primeras
A finales del siglo XVII, varias aristócratas y escritoras inglesas comenzaron a pedir una mejora en la educación de las mujeres. Poco después, apareció el primer almanaque dirigido a mujeres y repleto de matemáticas

Alfonso J. Población
El pasado mes de julio se celebraron en A Coruña las 19 JAEM ( Jornadas para el Aprendizaje y Enseñanza de las Matemáticas ), un evento de encuentro, intercambio de ideas y exposición de iniciativas entre profesores de matemáticas de todos los niveles. En esta ocasión las jornadas se articulaban en torno a siete núcleos temáticos, uno de los cuales era la Divulgación de las Matemáticas. Dentro de ese bloque presenté una ponencia titulada como esta sección, ABCdario de las Matemáticas , con el ánimo de darla a conocer.
Noticias relacionadas
Esa fue la idea inicial, pero también hice un pequeño repaso por algunos de los hitos más relevantes a lo largo de la historia de la divulgación de las matemáticas, hasta llegar a lo que puede considerarse una publicación pionera y bastante desconocida, el Diario de las Damas .
Los populares almanaques
En la primera parte del siglo XVIII, aparecen algunas revistas de matemáticas elementales, la mayoría incluyendo tímidamente, como con miedo ante la reacción, algún ejercicio matemático y, sobre todo, rompecabezas y cuestiones lúdico-recreativas dirigidas más al entretenimiento de sus lectores que al avance del conocimiento matemático. Como en prácticamente todo el mundo, desde la época de los griegos, también son muy populares los almanaques . Un almanaque consiste en un catálogo que comprende todos los días del año, con todo tipo de efemérides astronómicas, como entradas y salidas del Sol, principio de las estaciones, fases de la Luna, entrada en cada signo del Zodiaco, también datos relativos a hechos históricos, actos religiosos y civiles, principalmente de santos y festividades.
Eran imprescindibles para la agricultura ya que proporcionaban mucha información sobre estaciones y clima. En nuestro país fue (y es) muy popular el Calendario Zaragozano , por poner un ejemplo, aunque hay que volver a dejar claro que la mayor parte de su información no es de carácter científico, sino popular, costumbrista, fundamentada en refranes y usos populares, fundamentalmente.
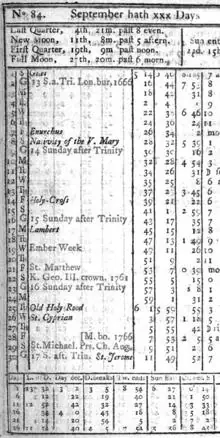
Pues bien, situémonos en Inglaterra, a finales del siglo XVII. Un grupo de aristócratas y escritoras inglesas , de diferentes ideas e intereses, comienzan a alzar sus voces para pedir una mejora en la educación de las mujeres (Hannah Woolley, Damaris Masham, Mary Astell, Mary Chudleigh, Mary Wortley Montagu, Elizabeth Thomas, Judith Drake, Elizabeth Elstob, entre otras muchas).
A decir verdad, la educación formal en aquel momento no contemplaba en absoluto a las mujeres , cuyas expectativas en la vida estaban reducidas a las tareas domésticas más básicas y elementales. Pero no nos equivoquemos. Aunque algunas referencias las citen como precursoras del feminismo, lo cierto es que no abogaban por la igualdad con los hombres (inimaginable en aquel momento); simplemente exigían que las chicas pudieran recibir una educación semejante a la de los varones, sin tener que hacerlo a escondidas y de forma autodidacta.
Tampoco hay que olvidar que la alfabetización matemática en el siglo XVIII era bastante deficiente para todos, hombres y mujeres. La educación en las escuelas inglesas estaba basada casi exclusivamente en la gramática latina; la aritmética elemental se consideraba adecuada solo para determinadas profesiones (comerciantes, mercaderes, marineros, carpinteros, agrimensores de tierras, o similares), por lo que fue completamente descuidada. Las matemáticas no se consideraban una asignatura para un buen académico ni eran parte de la educación de un joven gentleman.
El primer almanaque para mujeres
Con este panorama, en 1704, el maestro de escuela (especializado en matemáticas) y editor de almanaques John Tipper , concienciado con las reivindicaciones expuestas, decide publicar u no de estos almanaques dirigido específicamente a las mujeres . Durante los tres primeros años, además de los temas específicos que hemos mencionado de este tipo de publicaciones, añade otros, como recetas, bocetos de mujeres notables, artículos sobre salud y educación , etc, que en 1707 elimina para dejar paso a enigmas, consultas, cuestiones y preguntas matemáticas, de un amplio rango de ramas geometría, álgebra, astronomía, dinámica, fluxiones, armónicos, hidrostática, isoperimetría, navegación, óptica... Así hasta 25 categorías, cuando en la época lo más común era abordar asuntos como la medicina o la jardinería.
Pero Tipper no lo tuvo fácil: la publicación de todos los almanaques en Inglaterra estaba controlada por la Worshipful Company of Stationers , un monopolio instituido por decreto real, que marcaba una serie de condiciones como limitar el número de ejemplares (el primero no debía sobrepasar los 3.000 números) y en este caso particular, sólo por dedicarse a las mujeres, le exigieron un precio de venta superior al del mercado habitual para estas publicaciones. A pesar de todo el resultado fue espectacular: se convirtió en una de las revistas más longevas de Inglaterra (se editó durante más de un siglo, hasta 1840), llegó a vender más de 7.000 ejemplares algún año, llegaron a recibir hasta medio millar de cartas con soluciones a los problemas propuestos, y marcó un estilo que aún perdura en cuanto a las revistas de divulgación.
El estudio y análisis de las repercusiones de esta publicación (la primera que se sepa por el momento dirigida a las mujeres) aún está en marcha, aunque se conocen muchos detalles, algunos realmente llamativos. Se estima que el nivel social de los lectores era evidentemente de clase media-alta fundamentalmente, ya que eran los que tenían más tiempo y posibilidades de ocuparse de la resolución y elaboración de problemas. Se sabe más sobre los hombres y mujeres que contribuyeron al Diario de las Damas y otras revistas similares que de sus lectores.
La mayoría fueron hombres (de los 913 contribuyentes que figuran en los índices, solo 32 eran mujeres, es decir, un 3.5%), muchos relacionados con instituciones militares (sus estudios poseían muchos contenidos matemáticos aplicados). Sin embargo, se desconoce la verdadera identidad de muchos, ya que solían utilizar seudónimos o alias (por ejemplo, una de las más prolíficas, que firmaba como Ann Nichols, era en realidad un hombre del que sólo se sabe su apellido, Mr. Wales; en el porcentaje anterior sólo se han contemplado las que realmente se sabe que eran mujeres). Paradójicamente, todos los editores del Diario de las Damas fueron hombres, salvo uno: tras el fallecimiento en 1743 del segundo, Henry Beighton, su viuda, Caelia Beighton, asumió su trabajo hasta 1745.
Echemos un vistazo a alguna de las cuestiones propuestas en el Diario de las Damas. En la imagen observamos la cuestión 984, propuesta en 1795, y solucionada en 1796, por la señorita Nancy Mason, de Clapham, un barrio del municipio londinense de Lambeth.

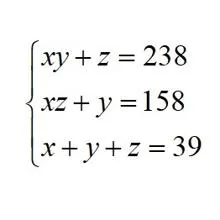
Queridas damas justas, solemnemente declaro
En la página de Día del próximo año.
Cuando primero fue, comenzó a pasar.
Mi tiempo en esta esfera.
Mi edad tan clara; el primer otro año
En años, en meses, y días
Con sencillez tú encontrarás, por lo que se adjunta*
Exacto el mismo se muestra
Bajo el asterisco, se adjunta la imagen de la derecha, donde x = los años, y = los meses, y z = los días de la edad , el primero de enero de 1795. Durante los primeros años se requería que los enunciados se enviaran en verso, aunque dejó de hacerse ante la queja de algunos lectores por la baja calidad de las rimas.
Si tratamos de resolverlo, comprobaremos que no es demasiado complicado, aunque eso sí, es un sistema no lineal (los sumandos xy, xz que aparecen hacen que no sea lineal; recuérdese que lineal significa que los exponentes de las incógnitas son de primer grado, y no hay productos entre ellas), y por tanto no hay un procedimiento sistemático para su resolución. No queda otra que despejar de una ecuación y sustituir en las otras para ver si se nos aclara la cosa. Yo lo que he hecho ha sido sumar las dos primeras ecuaciones (para tener el x + y + z, de la tercera ecuación, pero ya se sabe que cada maestrillo, …), y así tener la factorización (y + z)(x + 1) = 396. De ahí sustituyo y + z por 39 – x, y llegamos a una ecuación de segundo grado con una sola incógnita, que se resuelve sin problemas. De las dos soluciones nos quedamos con la de enteros positivos que resulta ser x = 21 años, y = 11 meses y z = 7 días, y tendremos la edad de la proponente a uno de enero de 1795 . Valore el lector la pertinencia de la propuesta para un público general.
Más ejercicios de la revista
Les dejo otros ejercicios de esas revistas, por si se animan:
985 .- Si una persona pide prestada cualquier suma de dinero al 5% por año a interés compuesto, y lo presta al mismo tiempo al 10% al año mediante interés simple, ¿cuándo será la diferencia de intereses la menor posible?
986. - Dentro de un jardín rectangular, cuya longitud es de 4 cadenas y su anchura 3 cadenas, hay un estanque de agua de forma trapezoidal, cuyos ángulos opuestos están alineados con los del jardín, y las distancias respectivas de los ángulos de uno desde los del otro, son 20, 25, 40 y 45 yardas, en orden creciente. Se requiere el área del estanque.
996. - Mr. T. Simpson (se refiere al matemático inglés Thomas Simpson, célebre por su famosa regla para aproximar numéricamente integrales definidas), en su libro sobre Álgebra ( Tratado sobre Álgebra , publicado en 1745), muestra cómo resolver ecuaciones bicuadráticas, reduciéndolas a la diferencia de dos cuadrados completos, y afirma que la mayor ventaja de este procedimiento es que el valor de A en la ecuación cúbica que resulta, es conmensurable y racional, no sólo cuando todas las raíces de la ecuación dada sean conmensurables, sino cuando son irracionales, e incluso imposibles (se refiere a complejas). ¿Es esta ventaja general para cualquier ecuación bicuadrática que tenga coeficientes racionales, como...
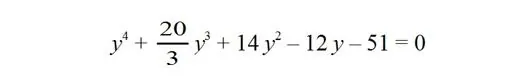
...o no es así? Dar una demostración de la afirmación.
1089. - Un péndulo vibra en un minuto tanto como indican las pulgadas de su longitud. ¿Cuál es dicha longitud?
1111. - Encontrar dos números tales que, si se suma una unidad a cualquiera de ellos, resultan cuadrados perfectos, y si se hace lo mismo a su suma y a su diferencia, también obtenemos cuadrados perfectos.
NOTICIA DEL VERANO:
En la reseña publicada el 8 de abril de este año sobre la ecuación diofántica x^3 + y^3 + z^3 = k, indicábamos que se había encontrado los valores de la terna (x, y, z) para uno de los dos únicos valores que faltaba encontrar para valores de k desde 1 a 100, el de k = 33. Sólo faltaba resolver la ecuación para k = 42, y animábamos a los lectores a intentar desvelar ese caso. Finalmente, un equipo formado por los profesores Andrew Booker, de la Universidad de Bristol, y Andrew Sutherland, del MIT, han encontrado gracias al trabajo en paralelo de medio millón de PCs la siguiente solución :
(–80538738812075974)^3 + (80435758145817515)^3 + (12602123297335631)^3 = 42

Alfonso Jesús Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la Real Sociedad Matemática Española (RSME).
El ABCdario de las Matemáticas es una sección que surge de la colaboración con la Comisión de Divulgación de la RSME.
Esta funcionalidad es sólo para registrados
Iniciar sesión